STUDY SESSION 1 - QUANTITATIVE METHODS
READING 3 - Probability Concepts
3.1. Conditional and Joint Probabilities
| Terms | (Random variable) - Uncertain quantity or number. (Outcome) - Observed value of a random variable. (Event) - Single outcome or a set of outcomes. (Mutually exclusive events) – Events that cannot happen at the same time. (Exhaustive events) – Events that include all possible outcomes. |
| Properties of Probability | - Probability of occurrence of any event (Ei) is between 0 and 1 - If a set of events is mutually exclusive and exhaustive, the probabilities of those events sum to 1. |
| Objective Probability | (Empirical Probability) –Established by analyzing past data or outcome. (Priori Probability) – Determined using a formal reasoning and inspection process(not data) |
| Subjective Probability | The least formal method of developing probabilities and involve the use of personal judgement. |
| Odds | The odds of an event represent the ratio of the (probability that the event will occur) / (probability that the event will not occur). |
| Unconditional Probability | The probability of an event regardless of the past or future occurrence of other events. |
| Conditional Probability | The occurrence of one event affects the probability of the occurrence of another event. * The probability of A given the occurrence of B. * A conditional probability of an occurrence is also called its likelihood. |
| Joint Probability | The probability that the two events will both occur. * Also referred as the multiplication rule of probability. |
| Addition Rule of Probability |
The probability that at least one of two events will occur. * B1, B2, … Bn is a mutually exclusive and exhaustive set of outcomes. |
| Joint Probability of Independent Events |
The multiplication rule is used to calculate the joint probability of any number of independent events. |
3.2. Conditional Expectations and Expected Value
| Independent Events | The occurrence of independent events has no influence on the occurrence of the others. |
| Total Probability Rule | Used to determine the unconditional probability of an event, given conditional probability. * B1, B2, … Bn is a mutually exclusive and exhaustive set of outcomes. or * Bc is read “the complement of B”, meaning “not B” * P(Bc) = 1 - P(B) |
| Expected Value of Random Variable | The weighted average of the possible outcomes for the variable. |
| Variance and Standard Deviation | Variance and standard deviation measure the dispersion of a random variable around its expected value. (Variance) : Calculated as the probability-weighted sum of the squared deviations from the mean(or expected value). (Standard Deviation) : Positive square root of the variance |
3.3. Portfolio Variance, Bayes, and Counting Problems
| Portfolio Expected Return | The expected return of a portfolio composed of n assets with weights(w) and expected returns(R).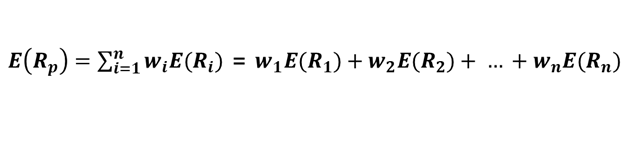 |
| Covariance | Measure of how two assets move together. * It is the expected value of the product of the deviations of the two random variables from their respective expected values. * Covariance of a random variable with itself is its variance of RA : Cov(RA,RA) = Var(RA) |
| Portfolio Variance | The asset weights, returns variances, and returns covariances are used to calculate the variance of portfolio returns.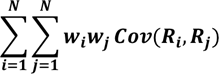 |
| Correlation | Correlation matrix to calculate portfolio returns variance. |
| Bayes' Formula | Used to update a given set of prior probabilities for a given event in response to the arrival of new information. |
| Labeling Formula | Refers to the situation where there are n items that can each receive one of k different labels. |
| Combination Formula |
The general formula for the two groups of label. * Number of possible ways of selecting r items from a set of n items * the order of selection is not important |
| Permutation Formula |
Different groups of size r in specific order from n objects. |
| Counting method | * The multiplication rule of counting is used when there are two or mor groups. * Factorial is used by itself when there are no groups. * The labeling formula applies to three or more subgroups of predetermined size. * The combination formula applies to only two groups of predetermined size where the order of selection is not important. * The permutation formula applies to only two groups of predetermined size where the order of selection is important. |
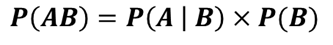
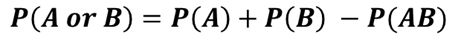
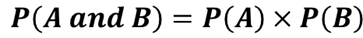
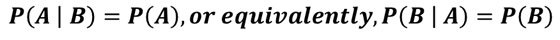
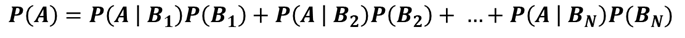
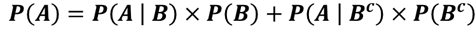
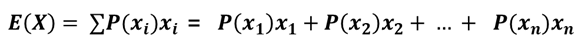
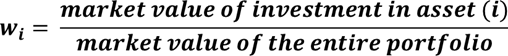
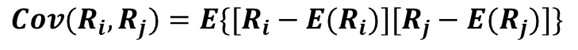
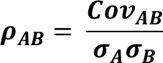
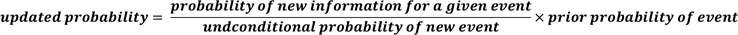
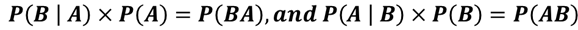

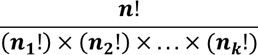
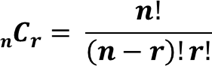
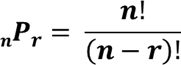
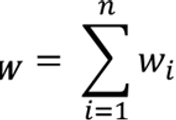

댓글